Shear Strain,Shear Stress, Shear Rate,Viscosity

Shear Strain:-

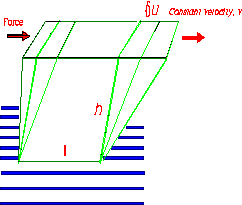
• To define the term STRAIN we will consider a cube of material with its base fixed to a surface as shown below in figure-1.

• If we now apply a constant 'pushing' force, F, to the upper part of the cube, assuming the material behaves as an ideal solid, it will obey Hooke's law of elastic deformation and will deform to a new position as shown in figure-1.
• This type of deformation (lower fixed upper moving) is defined as a SHEAR DEFORMATION.
• The deformation δ u and h are used to define the SHEAR STRAIN as :

                             Shear Strain =  δ u/h

• The shear strain is simply a ratio of two lengths (displacement / gap) and so has no units. It is important since it enables us to quote pre-defined deformations without having to specify sizes of sample etc

Shear Stress:-

• The SHEAR STRESS is defined as F/A (A is the area of the upper surface of the cube l x w) Since the units of force are Newtons and the units of area are m^2 it follows that the units of Shear Stress are N/M2 This is referred to as the PASCAL (i.e. 1 N/m^2 = 1 Pascal) and is denoted by the symbol σ (in older textbooks you may see it denoted as τ)

Shear Rate:-

• Consider the case of a cube of material that behaves as an ideal fluid. When we apply a shear stress (force) the material will continually deform at a constant rate as illustrated in figure-2.

• The rate of change of strain is referred to as the SHEAR STRAIN RATE often abbreviated to SHEAR RATE and is found by the rate of change of strain as a function of time i.e. the differential d.

       SHEAR STRAIN / d.TIME

Viscosity

• The Shear Rate obtained from an applied Shear Stress will be dependant upon the materials resistance to flow i.e. its VISCOSITY
• Since the flow resistance ≡ force / displacement it follows that ;

               VISCOSITY = SHEAR STRESS / SHEAR RATE

• The units of viscosity are Nm^2s   Which are better known as Pascal Seconds (Pa.s)
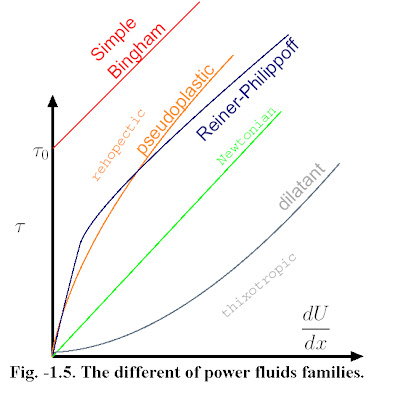
• If a material has a viscosity which is independent of shear stress then it is referred to as an ideal or NEWTONIAN fluid. The mechanical analogue of a Newtonian fluid is a viscous dashpot which moves at a constant rate when a load is applied as seen in figure-3.

Viscosity

The resistance of a fluid to flow

1 Ns/m^2 = 1 Pa.s = 10 Poise
Viscosity in Poise / Density = Kinematic viscosity in Stokes

Shear Stress

1 Pa = 1 N/m^2 = 10 dyn cm^-2

Kinematic Viscosity

The dynamic viscosity divided by density

Shear Rate

The rate of change of shear stress.  The velocity gradient perpendicular to the direction of shear flow (dv/dx).  Units 1/s or s-1

Shear Stress

The shear force per unit area

Shear Strain

A unit-less quantity, the relative displacement of the faces of a sheared body (for example a layer of fluid) divided by the distance between them.

Zero-shear Viscosity

The viscosity at the limit of low shear rate. The viscosity a product will ultimately attain when at rest and undisturbed.

Shear Stress

• The shear stress is part of the pressure tensor.
• However, here it will be treated as a separate issue.
•  In solid mechanics, the shear stress is considered as the ratio of the force acting on area in the direction of the forces perpendicular to area. 
• Different from solid, fluid cannot pull directly but through a solid surface. 
• Consider liquid that undergoes a shear stress between a short distance of two plates as shown in Figure (1.1).
• The upper plate velocity generally will be

                         U = f(A, F, h)...............................................(1.2)

• Where A is the area, the F denotes the force, h is the distance between the plates.
• From solid mechanics study, it was shown that when the force per area increases, the velocity of the plate increases also. 
• Experiments show that the increase of height will increase the velocity up to a certain range. 
• Consider moving the plate with a zero lubricant (h » 0) (results in large force) or a large amount of lubricant (smaller force).
• In this discussion, the aim is to develop differential equation, thus the small distance analysis is applicable.

• The viscosity coefficient is always positive. When n, is above one, the liquid is dilettante. 
• When n is below one, the fluid is pseudoplastic. 
• The liquids which satisfy equation (1.13) are referred to as purely viscous fluids. 
• Many fluids satisfy the above equation. Fluids that show increase in the viscosity (with increase of the shear) referred to as thixotropic and those that show decrease are called reopectic fluids (see Figure 1.5).
• Materials which behave up to a certain shear stress as a solid and above it as a liquid are referred as Bingham liquids. In the simple case, the “liquid side” is like Newtonian fluid for large shear stress.

Kinds of Fluids

• Some differentiate fluid from solid by the reaction to shear stress. It is a known fact said that the fluid continuously and permanently deformed under shear stress while solid exhibits a finite deformation which does not change with time. 
• It is also said that liquid cannot return to their original state after the deformation. 
• This differentiation leads to three groups of materials: solids and liquids. This test creates a new material group that shows dual behaviors; under certain limits; it behaves like solid and under others it behaves like liquid (see chart of Fluid mechanics). The study of this kind of material called rheology.
• It is evident from this discussion that when a liquid is at rest, no shear stress is applied.
• The fluid is mainly divided into two categories: liquids and gases. 
• The main difference between the liquids and gases state is that gas will occupy the whole volume while liquids has an almost fix volume. 
• The difference between a gas phase to a liquid phase above the critical point are practically minor.
• Hence, the pressure will not affect the volume of liquid. 
• In gaseous phase, any change in pressure directly affects the volume. The gas fills the volume and liquid cannot.

What is Fluid Mechanics?

• Fluid mechanics deals with the study of all fluids under static and dynamic situations.
• Fluid mechanics is a branch of continuous mechanics which deals with a relationship between forces, motions, and statical conditions in continuous material. 
• This study area deals with many and diversified problems such as surface tension, fluid statics, flow in enclose bodies, or flow round bodies (solid or otherwise), flow stability, etc.
• In fact, almost any action a person is doing involves some kind of a fluid mechanics problem. 
• Furthermore, the boundary between the solid mechanics and fluid mechanics is some kind of gray shed and not a sharp distinction (see chart of Fluid mechanics for the complex relationships between the different branches which only part of it should be drawn in the same time.). 
• For example, glass appears as a solid material, but a closer look reveals that the glass is a liquid with a large viscosity. 
• A proof of the glass “liquidity” is the change of the glass thickness in high windows in European Churches after hundred years. 
• The bottom part of the glass is thicker than the top part. Materials like sand (some call it quick sand) and grains should be treated as liquids. It is known that these materials have the ability to drown people. 
• Even material such as aluminum just below the mushy zone also behaves as a liquid similarly to butter. 
• After it was established that the boundaries of fluid mechanics aren’t sharp, the discussion in this book is limited to simple and (mostly) Newtonian (sometimes power fluids) fluids which will be defined later.
• The fluid mechanics study involve many fields that have no clear boundary between them. 
• Researchers distinguish between orderly flow and chaotic flow as the laminar flow and the turbulent flow. 
• The fluid mechanics can also be distinguish between a single phase flow and multiphase flow (flow made more than one phase or single distinguishable material). 
• The last boundary (as all the boundaries in fluid mechanics) isn't sharp because fluid can go through a phase change  condensation or evaporation) in the middle or during the flow  and switch from a single phase flow to a multi phase flow. 
• Moreover, flow with two phases (or materials) can be treated as a single phase (for example, air with dust particle).

History of Fluid Mechanics

• The first progress in fluid mechanics was made by Leonardo Da Vinci (1452-1519) who built the first chambered canal lock near Milan. He also made several attempts to study the flight (birds) and developed some concepts on the origin of the forces. 
• After his initial work, the knowledge of fluid mechanics (hydraulic) increasingly gained speed by the contributions of Galileo, Torricelli, Euler, Newton, Bernoulli family, and D’Alembert. 
• At that stage theory and experiments had some discrepancy. This fact was acknowledged by D’Alembert who stated that, “The theory of fluids must necessarily be based upon experiment.” For example the concept of ideal liquid that leads to motion with no resistance, conflicts with the reality.
• This discrepancy between theory and practice is called the “D’Alembert paradox” and serves to demonstrate the limitations of theory alone in solving fluid problems. 
• As in thermodynamics, two different of school of thoughts were created: the first be-lieved that the solution will come from theoretical aspect alone, and the second believed that solution is the pure practical (experimental) aspect of fluid mechanics.
• On the theoretical side, considerable contribution were made by Euler, La Grange, Helmhoitz, Kirchhoff, Rayleigh, Rankine, and Kelvin. 
• On the “experimental” side, mainly in pipes and open channels area, were Brahms, Bossut, Chezy, Dubuat, Fabre, Coulomb, Dupuit, d’Aubisson, Hagen, and Poisseuille. 
• In the middle of the nineteen century, first Navier in the molecular level and later Stokes from continuous point of view succeeded in creating governing equations for real fluid motion. 
• Thus, creating a matching between the two school of thoughts: experimental and theoretical. But, as in thermodynamics, people cannot relinquish control. As results it created today “strange” names: Hydrodynamics, Hydraulics, Gas Dynamics, and Aeronautics.
• The Navier-Stokes equations, which describes the flow (or even Euler equations), were considered unsolvable during the mid nineteen century because of the high complexity. 
• At the end of the twenty century, the demand for vigorous scientific knowledge that can be applied to various liquids as opposed to formula for every fluid was created by the expansion of many industries. 
• This demand coupled with new several novel concepts like the theoretical and experimental researches of Reynolds, the development of dimensional analysis by Rayleigh, and Froude’s idea of the use of models change the science of the fluid mechanics. 
• While the understanding of the fundamentals did not change much, after World War Two, the way how it was calculated changed. 
• The introduction of the computers during the 60s and much more powerful personal computer has changed the field. There are many open source programs that can analyze many fluid mechanics situations. 

Chart for Fluid Mechanics