Shear Stress

• The shear stress is part of the pressure tensor.
• However, here it will be treated as a separate issue.
•  In solid mechanics, the shear stress is considered as the ratio of the force acting on area in the direction of the forces perpendicular to area. 
• Different from solid, fluid cannot pull directly but through a solid surface. 
• Consider liquid that undergoes a shear stress between a short distance of two plates as shown in Figure (1.1).
• The upper plate velocity generally will be

                         U = f(A, F, h)...............................................(1.2)

• Where A is the area, the F denotes the force, h is the distance between the plates.
• From solid mechanics study, it was shown that when the force per area increases, the velocity of the plate increases also. 
• Experiments show that the increase of height will increase the velocity up to a certain range. 
• Consider moving the plate with a zero lubricant (h » 0) (results in large force) or a large amount of lubricant (smaller force).
• In this discussion, the aim is to develop differential equation, thus the small distance analysis is applicable.

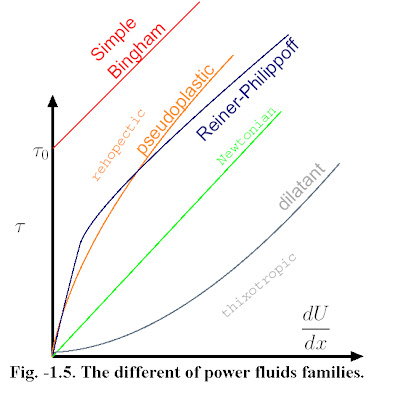
• The viscosity coefficient is always positive. When n, is above one, the liquid is dilettante. 
• When n is below one, the fluid is pseudoplastic. 
• The liquids which satisfy equation (1.13) are referred to as purely viscous fluids. 
• Many fluids satisfy the above equation. Fluids that show increase in the viscosity (with increase of the shear) referred to as thixotropic and those that show decrease are called reopectic fluids (see Figure 1.5).
• Materials which behave up to a certain shear stress as a solid and above it as a liquid are referred as Bingham liquids. In the simple case, the “liquid side” is like Newtonian fluid for large shear stress.